Introduction
As a postscript to the previous post, I set the following puzzle:
You’ve got a match ticket in a small section of the Gtech Community Stadium that has 100 seats. Each ticket is assigned to a specific seat and spectators take their seat one at a time. However, one of the other 99 attendees – let’s, for argument’s sake, call him Matthew – decides to sit in a random seat selected from those that haven’t yet been occupied. All other ticket-holders will sit in their assigned seat unless it’s already taken, in which case they sit in a random seat among those still unoccupied. You are the last person in the queue to take your seat; Matthew is in some random position in front of you in the queue. What’s the probability you end up sitting in the seat to which you’ve been assigned?
Many thanks to those of you who sent solutions – Fabian T, Paul W, Paul B, Louis P, Ben M, and Steve M. (Thanks especially to Steve and Paul B, for whom this sort of stuff is off-topic). Special thanks also to Anders, who is following the blog from outside the Smartodds universe, but was kind enough to reply anyway.
As Fabian pointed out, the puzzle is essentially one that is well-known, usually rewritten in terms of a drunk on a plane who – unlike all other passengers – chooses a seat at random rather than his allowed seat. Now, personally, I don’t think ‘Drunk on a Plane’ is a very flattering way to describe the esteemed owner of Smartodds and Brentford FC, but I’m just the messenger and can’t take responsibility for any offence caused.
Anyway, remarkably, the solution to the puzzle is 1/2. Even more remarkable – and this is what makes the puzzle so beautiful – is that the answer is 1/2, regardless of how many seats are available. Just think about that for a second: the answer isn’t just a simple number like 1/2, but it would have been that same simple number if I’d said there were 1000 or a million people in the queue.
Fundamentally, there are 2 alternative ways to arrive at the solution.
A Conceptual Solution
There are two seats of special interest – Matthew’s and yours. We’ll label them M and Y. Now, suppose Matthew is in position k in the queue; you are in position 100. Suppose also that Matthew is wearing a t-shirt that says ‘I am Matthew’. The (k-1) people in the queue before Matthew all take their own seats. According to the rules of the puzzle, Matthew then takes a random seat from those available. There are 3 possibilities for this action:
- It could be Matthew’s seat, M;
- It could be your seat, Y;
- It could be someone else’s seat.
Options 1 and 2 are equally likely, so if we know one of those events occurred, the probability that you get your seat is 1/2. If option 3 occurs, Matthew takes someone else’s seat – for argument’s sake, let’s suppose this person is called Cliff. Let’s also suppose that Matthew takes off his ‘I am Matthew’ t-shirt and gives it to Cliff. At this point there are (100 - k) people in the queue, and somewhere in that queue is Cliff, who becomes the ‘new Matthew’. The people in the queue in front of Cliff will now take their seats, and once Cliff gets to randomly select his seat – since his nominated seat has already been taken – he will have the same 3 options as above. And again, if he goes for options 1 or 2 it’s 50/50 whether you get your seat, otherwise he takes someone else’s seat and passes them the t-shirt. They then become the ‘new Matthew’ and the process continues, again with a shorter queue.
Eventually this process is bound to stop – one of the ‘Matthews’ will choose options 1 or 2, or the queue will consist of just you and ‘Matthew’ – and in either case you will get your seat if ‘Matthew’ selects his, for which the probability is 1/2.
A Formal Probability Solution
This time, let’s look at the queue from your point of view at the back, and suppose that Matthew is k places ahead of you. Let p_k be the probability that you get your seat in this situation. We need to show that p_k = 1/2 for all values of k .
Clearly p_1 = 1/2 : if Matthew is just one place ahead of you in the queue, he’ll take his seat or yours, each with probability 1/2.
Now, suppose we’ve already shown that p_k = 1/2 for some value of k , and consider the case that Matthew is (k+1) places ahead. Again, 3 things can occur:
- Matthew takes his own seat.
- Matthew takes your seat.
- Matthew takes someone else’s seat.
The first 2 of these outcomes each occur with probability 1/(k+1) , while option 3 will occur with probability (k-1)/(k+1) . If option 1 occurs you will definitely be able to take your seat. If option 2 occurs, you will definitely be unable to take your seat. If option 3 occurs, you might or might not be able to take your seat, depending on the option taken by the next person in the queue, who is k places ahead of you. It follows that
p_{k+1} = 1/(k+1) + 0 + (k-1)/(k+1) \times p_k
and if we substitute in the assumed value of p_k= 1/2 , we find p_{k+1} =1/2.
We’ve already shown p_1=1/2 . So, from this recursive relation it follows that p_2=1/2 . From which it follows that p_3=1/2 . Then p_4 and so on and so on. This type of proof is termed mathematical induction.
Discussion and Extensions
You might prefer either the conceptual or formal probability solution to the problem, but in both cases there was no reference to the fact that there were actually 100 people in the queue. So the proofs would have been equally valid regardless of how many people were in the queue, leading, as I say, to the remarkable fact that the solution is 1/2 for queues of any length.
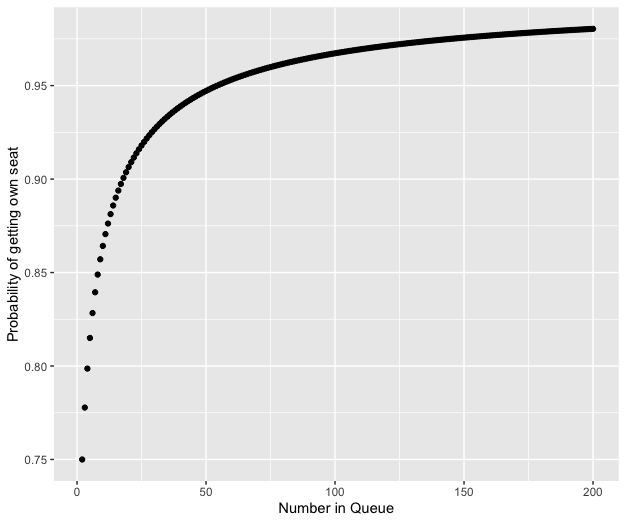
Now, actually, I made a slip when I first sent the post, thinking the puzzle could be easily solved in a more general setting. So in place of ‘You are the last person in the queue to take your seat; Matthew is in some random position in front of you in the queue’, I originally wrote ‘You and Matthew are both in random places in the queue’. I mis-calculated though, and the puzzle stated this way is more difficult than I realised or intended. Despite this, puzzle-king Fabian still managed to provide a solution. In this case, the answer does depend on how many people are in the queue. With just 2 people in the queue the answer is 0.75: with probability 1/2 you’re ahead of Matthew in the queue and can take your seat. With probability 1/2 you’re behind him, but if that occurs there’s a probability of 1/2 that Matthew takes his own seat, in which case you still get yours. So in this case, the probability is
1/2 + (1/2 \times 1/2) = 3/4
Fabian generalised this argument, leading to a formula for the probability as a function of the number of people in the queue. With 100 people in the queue, the probability that you get your seat is around 0.967. More generally, the probability can be read from the following graph:
Fabian also posed the question – and provided a partial solution – as to what the answer would be if there were several drunks on the plane, but I think he’s caused enough offence for one day, without now going on to pass comment on Smartodds employees flying off on a serious work-oriented offsite meeting.
