In the spirit of Christmas, this post contains a statistical puzzle and a link to other puzzles that, while not explicitly statistical themselves, do have a connection with Statistics. I’ll post a solution to the first puzzle and comments about the others sometime next month.
Secret Santa
Five members of the Smartodds Quant team have formed a Secret Santa group this year: each of the five has to buy a present that will be randomly allocated to someone in the group by placing the five members names into a hat. Then, each person randomly selects one of the names from the hat, and that will be the group member for whom they are the Secret Santa.
But this scheme has an obvious fault: one or more members of the group might draw their own name from the hat, in which case they will be allocated the present they bought themselves.
So, three questions:
- What’s the probability that this scheme will actually work out ok, without anyone in the group being allocated their own present?
- For a hardcore bonus point, what would this probability be if there were 10 people in the group, rather than just five?
- And for a super hardcore bonus point, what if there were infinitely many people in the group?
I’ll post the solution to this problem, with discussion, in a couple of weeks. Meantime, I’d be very happy to receive your own solutions, even if based on guesswork.
GCHQ festive quiz
If you want more festive puzzles, though not strictly connected to Statistics, GCHQ – the UK’s intelligence agency – produces a festive quiz for schools every year. Here’s a video explaining this year’s quiz, which can be downloaded here.
Just to get you in the mood, here’s a puzzle from the GCHQ quiz of several years ago.
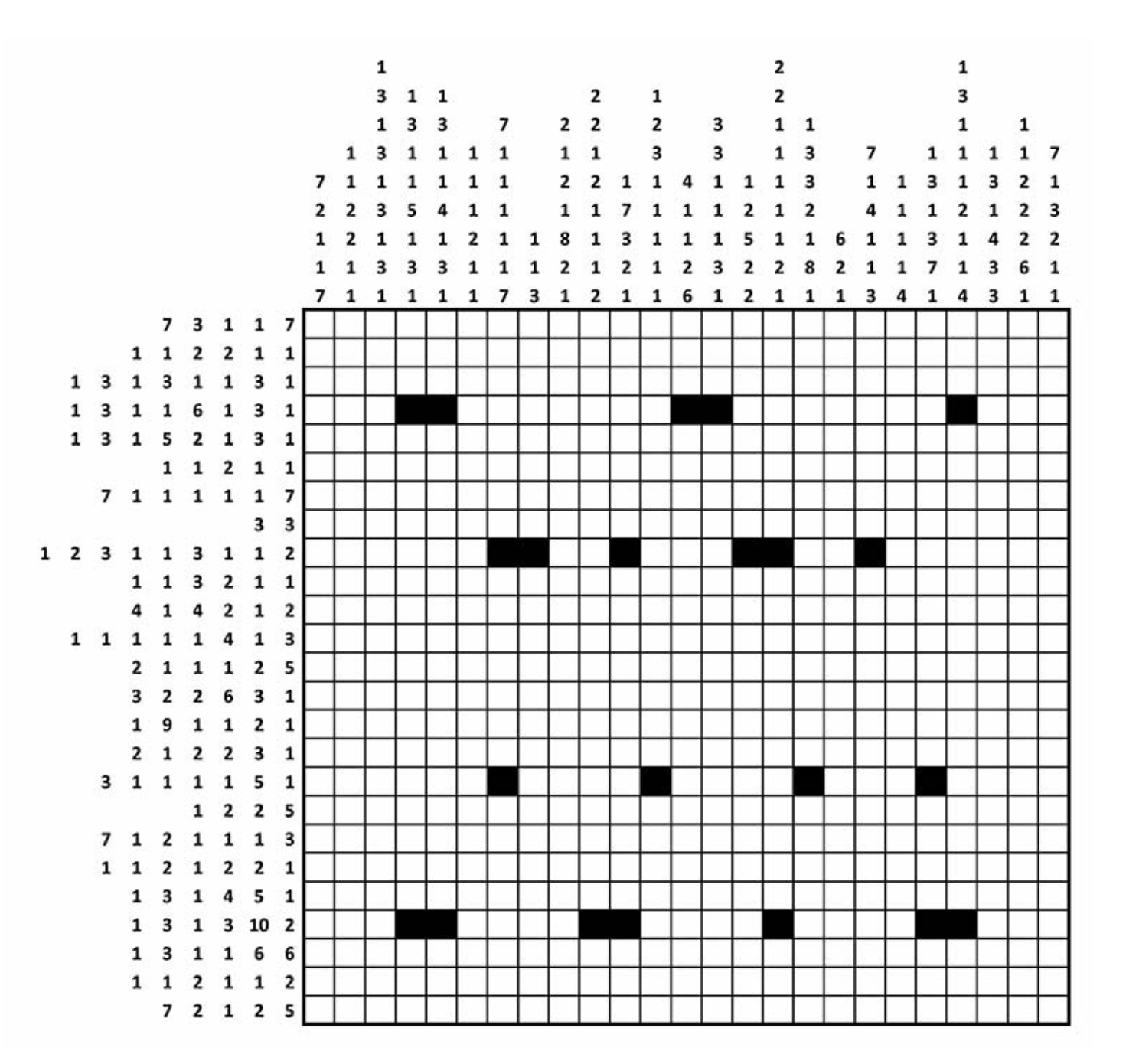
It’s an example of a nonogram. Each cell in the grid should be shaded black or left unshaded. The numbers attached to each row and column are shading instructions. Specifically, they tell you the lengths of blocks of cells to be shaded black in that particular row or column. For example, the numbers in the first row are 7,3,1,1,7. This means there are 5 distinct shaded blocks in that row, having lengths 7, 3, 1, 1 and 7 cells respectively, in that order from left to right. A few of the cells have been shaded already, Your task is to complete the shading of the whole grid according to the codes in the row and column numbers. The solution is a surprise that will lead you to some more puzzles.
(Update: Solutions to this year’s quiz are already available here).
RSS Christmas quiz
Finally, as I’ve mentioned before, the Royal Statistical Society publishes its own quiz every Christmas, and it has the reputation of being ‘the toughest out there’. This year’s version is here.
The competition is open to anyone – not just RSS members – and the first prize is a staggering £100 in book tokens. Moreover, the RSS will make a donation to the charity of your choice if you submit an entry scoring 30% or more.
To give you an idea of how it works, this is last year’s quiz, for which the solutions are here.
It’s not for the faint hearted, so good luck if you go for it.
Solutions and Comments
The answer to the Secret Santa puzzle when there are 5 people in the group is 11/30, or approximately 0.367.
To see this, label the group members A, B, C, D and E. Each person in the group selects a name from the hat. We can label these by the names of the person providing the gift. So, for example, the arrangement
B, D, C, E, A
would correspond to A getting the gift from B, B getting the gift from D, C getting their own gift, D getting the gift from E, and E getting the gift from A.
It’s well known that the number of such arrangements is
5! = 5 x 4 x 3 x 2 x 1 = 120
That’s because the first person could get the gift from 5 different people, leaving 4 choices for the second person, and so on.
However, an arrangement like B, D, C, E, A means that at least one of the individuals gets their own gift. By contrast, an arrangement like
B, D, E, A, C
would imply each individual getting a different one from the one they provided. An arrangement of this type. where each of the letters is in a different place with respect to the names of the gift receivers
A, B, C, D, E
is called a derangement. Since all arrangements are equally likely by the randomisation process of putting names in a hat and blindly extracting, it follows that the probability that the Secret Santa ‘works’ i the sense of all participants receiving a different gift from the one they provide is simply the proportion of derangements among the complete set of arrangements. We know there are 120 arrangements, so it remains just to count the derangements. It’s not too difficult a task to list all of the derangements – like B, D, C, E, A – and it turns out there are 44 of them. It follows that the probability of a successful Secret Santa program is 44/120 or 11/30.
In general, with n participants, the number of arrangements is written as n!. The number of derangements of n objects has a similar notation !n, so in general the probability that a group of n participants will have a successful Secret Santa is
n!/!n
The calculation of n! is the equivalent of that shown above for 5!, and therefore easy for all values of n. The calculation of !n is less obvious. As discussed above, with n = 5, it’s not too difficult to list all of the options and find !5 = 44. But with n = 10, say, this already becomes impractical. Fortunately, as explained in the wikipedia page for derangements, there is a standard formula which enables the calculation of !n for any value of n. In the case of n = 10, it leads to
!10 = 1,334,961
Then, since 10! = 3,628,800, it follows that the probability of a successful Secret Santa with 10 participants is
1,334,961/ 3,628,800 = 0.368
The wikipedia article also gives a neat proof of the formula for !n and shows that for large n the value of !n is approximately n!/e where e is the so-called Euler’s number, equal to roughly 2.7183. It follows that for large n, the probability of a successful Secret Santa is
1/e
and, in technical terms, this is the exact probability as the number of participants approaches infinity. In actual fact, 1/e is a very good approximation to the answer with a value of n as small as 5, so the limiting value is reached very quickly. That’s to say, even with just 5 participants, the probability of a successful program isn’t much different from that you’d get with infinitely many participants.
Kudos and brownie points to Milt and Louis who each sent me model solutions, with slight variations on the way to prove the general formula for !n. Very clever. Thanks also to Anders who lives outside of the Smartodds-verse, but was still kind enough to send me his solution which relied more on intuition, but still hit the nail (almost) on the head.
The Secret Santa puzzle is actually a slight modification of a problem that originally appeared in the Riddler, which until it stopped recently was a weekly puzzle column included in Nate Silver’s FiveThirtyEight website, which is a great resource for many aspects of statistics (especially those connected to U.S. elections). Many of the puzzles have also been collected into a book, available here. If you like puzzles of the Secret Santa type, I highly recommend it.
Finally, this is the solution to the GCHQ festive quiz nonogram:

As you will see, the solution is actually a QR code, which will actually lead you to a set of new puzzles.
